数位dp | Aquabet

前言

数位dp就是套模板 ——lwz^[0]

本文将通过对模板本身进行分析，以及通过一些例题来了解如何使用模板来解决问题。
既然是模板，首先当然要清楚数位dp可以用来解决什么样的问题。总结来说，数位dp可以用于解决在给定区间 $[A,B]$ 内，符合条件 $f(i)$ 的数 $i$ 的个数。条件 $f(i)$ 一般与数的大小无关，而与数的组成有关。如同其名字一样，数位dp便是按照数位来进行dp状态的分析和转移。数位dp解决的问题很多时候看起来很简单，甚至直接的暴力方法都仅有$O(n)$的时间复杂度。但是当这些问题的规模变大，即当 $n$ 在 $10^{19}$ 的级别下，$O(n)$的时间复杂度就完全无法应对，而数位dp是按位dp，数的大小对复杂度的影响很小，很多情况下能够达到$O(log(n))$级别，用来解决这样的问题再合适不过了。

从起点向下搜索，到最底层得到方案数，一层一层向上返回答案并累加，最后从搜索起点得到最终答案。这便是数位dp解决问题的过程。而对于 $[l,r]$ 区间问题，我们一般把他转化为两次数位dp,即找 $[0,r]$ 和 $[0,l-1]$ 两段，再将结果相减就得到了我们需要的 $[l,r]$。

如同大多数dp一般，数位dp有两种实现方式，递推和记忆化搜索。我个人更喜欢记忆化搜索，同时相比递推方式，记忆化搜索更适合作为模板，因此接下来的数位dp的模板以记忆化搜索的形式呈现。

题目1

首先我们从这道题开始了解数位dp：leetcode 233题

题目描述

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

示例 1：
输入：n = 13
输出：6
示例 2：
输入：n = 0
输出：0
提示：
$0 <= n <= 10^9$

代码

这道题在leetcode上的标签是困难。$10^9$的数据范围，使得直接的暴力算法无法达到要求。从这道条件比较简单的题开始，对模板涉及到的内容进行分析。先附上AC代码，并将其作为基础模板：

class Solution {
public:
int dp[15][15];
int num[15];
int dfs(int pos, int sum, int limit) {
    if(pos == 0) {
        return sum;
    }
    if(limit == 0 && dp[pos][sum] != -1) {
        return dp[pos][sum];
    }
    int up = 9;
    if(limit == 1) {
        up = num[pos];
    }
    int ans = 0;
    for(int i = 0; i <= up; i++) {
        ans = ans + dfs(pos-1, sum+(i == 1), i == up && limit);
    }
    if(limit == 0) {
        dp[pos][sum] = ans;
    }
    return ans;
}
    int countDigitOne(int n) {
    int pos = 0;
    while(n != 0) {
        pos++;
        num[pos] = n % 10;
        n = n / 10;
    }
    memset(dp, -1, sizeof(dp));
    return dfs(pos, 0, 1);
    }
};

// 执行用时: 0 ms
// 内存消耗: 5.9 MB

分析

从核心的dfs部分开始看。dfs部分 dfs(int pos,int sum,int limit) 涉及到三个参数，pos，sum以及limit。其中pos表示当前的数位，我们从最高位开始进行dp，sum表示当前状态数码1的个数，是对应这道题目要求而增添的变量，limit表示当前状态是否达到最高位限制。这三个参数中，需要进行解释的主要是limit参数。

最高位标记`limit`

在搜索的数位的过程中，搜索范围可能发生变化。

举个例子：我们在搜索 [0,555] 的数时，显然最高位搜索范围是 0 ~ 5 ，而后面的位数的取值范围会根据上一位发生变化：

当最高位是 1 ~ 4 时，第二位取值为 [0,9]；

当最高位是 5 时，第二位取值为 [0,5] （再往上取就超出右端点范围了）

为了分清这两种情况，我们引入了 limit 标记：

若当前位 limit = 1 而且已经取到了能取到的最高位时，下一位 limit = 1 ；
若当前位 limit = 1 但是没有取到能取到的最高位时，下一位 limit = 0 ；
若当前位 limit = 0 时，下一位 limit = 0 。

int up = 9;
if(limit == 1) {
    up = num[pos];
}
int ans = 0;

这一部分中的up便是表示当前能取到的最高位数，下一位limit的状态自然是i == up && limit。
接下来还有一个需要分析的地方：

if(limit == 0 && dp[pos][sum] != -1) {
    return dp[pos][sum];
}
if(limit == 0) {
    dp[pos][sum] = ans;
}

也就是dp值的保存和取用问题。

举个例子：
假设存在如下约束：数位上不能出现连续的两个1(11、112、211都是不合法的)
假设就是$[1,210]$这个区间的个数
状态dp[pos][pre]:当前枚举到pos位，前面一位枚举的是pre(更加前面的位已经合法了)，的个数(假设pos从0开始)。

先看错误的方法计数，就是不判limit直接dfs。

那么假设我们第一次枚举了百位是0，显然后面的枚举limit = false，也就是数位上0到9的枚举，然后当我十位枚举了1，此时考虑dp[0][1],就是枚举到个位，前一位是1的个数，显然dp[0][1]=9;(个位只有是1的时候是不满足的)，这个状态记录下来，继续dfs，一直到百位枚举了2，十位枚举了1，显然此时递归到了pos=0,pre=1的层，而dp[0][1]的状态已经有了即dp[pos][pre] != -1；此时程序直接return dp[0][1]了，然而显然是错的，因为此时是有limit的个位只能枚举0，根本没有9个数，状态之间存在冲突。(也可以从上面第一题从数学的角度分析一下，我们记录的是0~9这样的重复状态，而limit == 1实际上是属于特殊状态)因此我们可以得到一个结论：当 limit = 1 时，不能记录和取用dp值。
类似上述的分析过程，我们也可以得出：当 lead = 1 时，也不能记录和取用dp值。(lead用于表示前导零，在后面会讲到，提到时可以翻回来看看)
当然也没有这么绝对，一起都是以实际题目为准。
由此我们发现，模板中需要根据实际情况修改的部分就是下面这一部分：

1
2
3

for(int i=0;i <= up;i++) {
    ans = ans + dfs(pos-1, sum+(i == 1), i == up && limit);
}

根据实际题目要求，修改其中的约束条件，就可以利用模板来解决问题了。
接下来再看看另一个重要参数，也就是前面提到的lead。

前导0标记`lead`

举个例子：假如我们要从 $[0,1000]$ 找任意相邻两数相等的数。

显然 111,222,888 等等是符合题意的数
但是我们发现右端点 1000 是四位数
因此我们搜索的起点是 0000 ，而三位数的记录都是 0111,0222,0888 等等
而这种情况下如果我们直接找相邻位相等则 0000 符合题意而 0111,0222,0888 都不符合题意了
所以我们要加一个前导0标记

如果当前位 lead = 1 而且当前位也是0，那么当前位也是前导0， pos + 1 继续搜；
如果当前位 lead = 1 但当前位不是0，则本位作为当前数的最高位， pos + 1 继续搜；（注意这次根据题意其他参数可能发生变化）

当然前导 0 有时候是不需要判断的，上述的例子是一个有关数字结构上的性质，0会影响数字的结构，所以必须判断前导0；而如果我们研究的是数字的组成（例如这个数字有多少个 1 之类的问题），0并不影响我们的判断，这样就不需要前导0标记了。

题目2

接下来看一个前导零的例子：leetcode 902

题目描述

我们有一组排序的数字 D，它是 {‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’} 的非空子集。（请注意，’0’ 不包括在内。）
现在，我们用这些数字进行组合写数字，想用多少次就用多少次。例如 D = {‘1’, ‘3’, ‘5’}，我们可以写出像 ‘13’, ‘551’, ‘1351315’ 这样的数字。
返回可以用 D 中的数字写出的小于或等于 N 的正整数的数目。

示例 1：
输入：D = [“1”,”3”,”5”,”7”], N = 100
输出：20
解释：
可写出的 20 个数字是：
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.
示例 2：
输入：D = [“1”,”4”,”9”], N = 1000000000
输出：29523
解释：
我们可以写 3 个一位数字，9 个两位数字，27 个三位数字，81 个四位数字，243 个五位数字，729 个六位数字，2187 个七位数字，6561 个八位数字和 19683 个九位数字。总共，可以使用D中的数字写出 29523 个整数。
提示：
D 是按排序顺序的数字 ‘1’-‘9’ 的子集。$1 <= N <= 10^9$

代码

class Solution {
public:
int in[10];
int dp[15];
int nums[15];
int dfs(int pos,int limit,int lead) {
    if(pos == 0)  return !lead;
    if(limit == 0 && lead == 0 && dp[pos] != -1)  return dp[pos];
    int up = 9;
    if(limit == 1) up = nums[pos];
    int ans = 0;
    for(int i = 0; i <= up; i++) {
        if(lead == 1 && i == 0) {
            ans = ans + dfs(pos-1, limit && i == up, lead && i == 0);
        }
        else if(in[i] == 1) {
            ans = ans + dfs(pos-1, limit && i == up, lead && i == 0);
        }
    }
    if(limit == 0 && lead == 0)  dp[pos] = ans;
    return ans;
}
    int atMostNGivenDigitSet(vector<string>& digits, int n) {
    int size = digits.size();
    memset(dp, -1, sizeof(dp));
    memset(in, 0, sizeof(in));
    for(int i = 0; i < size; i++) {
        in[digits[i][0]-'0'] = 1;
    }
    int pos = 0;
    while(n != 0) {
        pos++;
        nums[pos] = n % 10;
        n = n / 10;
    }
    return dfs(pos, 1, 1);//最高位默认有前导零
    }
};

分析

其中

if(lead == 1 && i == 0) {
    ans = ans + dfs(pos-1, limit && i == up, lead && i == 0);
} else if(in[i] == 1) {
    ans = ans + dfs(pos-1, limit && i == up, lead && i == 0);
}

便是增加前导零后的处理逻辑的变化，至于具体的要根据实际情况来进行变化。
另外对于状态的记录，最好把所有的额外状态都进行记录，避免状态存在重复和遗漏。虽然这会增加记录数组的维数，但是一般增加的状态都是0,1状态，所以内存方面不会有太多的压力。

数位dp的状态能记录的最好都记录上 ——lwz

附上洛谷制作的搜索步骤的图：

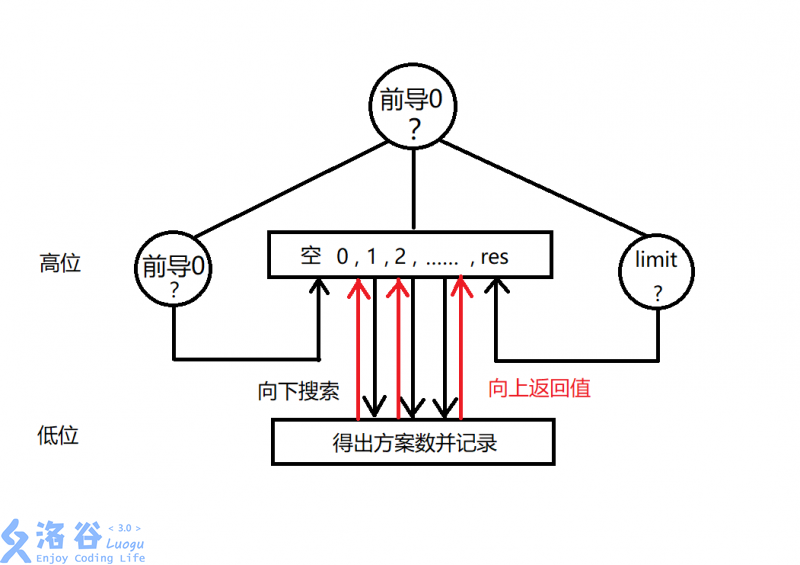
接下来就可以利用模板刷题了，随着使用的次数++，熟练度也会不断++的。数位dp说难也难，说难也不难，通过大量的练习就可以熟练掌握。

题目3

HDU3555

题目描述

The counter-terrorists found a time bomb in the dust. But this time the terrorists improve on the time >bomb. The number sequence of the time bomb counts from 1 to N. If the current number sequence >includes the sub-sequence “49”, the power of the blast would add one point.
Now the counter-terrorist knows the number N. They want to know the final points of the power. Can you help them?
Input
The first line of input consists of an integer T (1 <= T <= 10000), indicating the number of test cases. >For each test case, there will be an integer N (1 <= N <= 2^63-1) as the description.
The input terminates by end of file marker.
Output
For each test case, output an integer indicating the final points of the power.

Sample Input
3
1
50
500
Sample Output
0
1
15
Hint
From 1 to 500, the numbers that include the sub-sequence “49” are “49”,”149”,”249”,”349”,”449”,”490”,”491”,”492”,”493”,”494”,”495”,”496”,”497”,”498”,”499”,so the answer is 15.

分析&&代码

因为查找的数是一个两位数，所以我们增加pre参数，表示当前数位的前一位，来帮助进行约束判断。AC代码如下：

#include<bits/stdc++.h>
using namespace std;
long long num[30];
long long dp[30][20][2];
long long dfs(long long pos, long long pre, long long limit, long long check)
{
    if(pos == 0) {
        return check;
    }
    if(limit == 0 && dp[pos][pre][check] != -1) {
        return dp[pos][pre][check]
    }
    long long up = 9;
    if(limit == 1) {
        up = num[pos];
    }
    long long ans = 0;
    for(long long i = 0; i <= up; i++) {
        ans = ans + dfs(pos-1, i, i == up && limit, ((i == 9) && (pre == 4)) || check);
    }
    if(limit == 0) {
        dp[pos][pre][check] = ans;
    }
    return ans;
}

int main()
{
    long long t;
    cin >> t;
    memset(dp, -1, sizeof(dp));
    for(long long i = 0; i < t; i++) {
        long long x;
        cin>>x;
        long long pos = 0;
        while(x != 0) {
            pos++;
            num[pos] = x % 10;
            x = x / 10;
        }
        cout<<dfs(pos, 0, 1, 0)<<endl;
    }
    return 0;
}

PS：这题要爆int，记得开long long。

题目4

最后再来道家乡の题: [CQOI2016]手机号码

题目描述

人们选择手机号码时都希望号码好记、吉利。比如号码中含有几位相邻的相同数字、不含谐音不吉利的数字等。手机运营商在发行新号码时也会考虑这些因素，从号段中选取含有某些特征的号码单独出售。为了便于前期规划，运营商希望开发一个工具来自动统计号段中满足特征的号码数量。
工具需要检测的号码特征有两个：号码中要出现至少 3 个相邻的相同数字；号码中不能同时出现 8 和 4。号码必须同时包含两个特征才满足条件。满足条件的号码例如：13000988721、23333333333、14444101000。而不满足条件的号码例如：1015400080、10010012022。
手机号码一定是 11 位数，前不含前导的 0。工具接收两个数 L 和 R，自动统计出 [L,R] 区间内所有满足条件的号码数量。L 和 R 也是 11 位的手机号码。
输入格式
输入文件内容只有一行，为空格分隔的 2 个正整数 L,R。
输出格式
输出文件内容只有一行，为 1 个整数，表示满足条件的手机号数量。

输入样例
12121284000 12121285550
输出样例
5
说明/提示
样例解释：满足条件的号码： 12121285000、 12121285111、 12121285222、 12121285333、 12121285550。

数据范围：$10^{10} \le L\le R < 10^{11}$

分析&&代码

只需要增加check8，check4，连续段检查三个状态，同时注意前导零的处理就可以了。~~早生几年我也能混进省队了~~
AC代码如下：

#include <bits/stdc++.h>
using namespace std;
long long dp[20][20][20][2][2][2];
long long num[60];
long long dfs(long long pos, long long pre1, long long pre2, long long limit, long long lead, long long check8, long long check4, long long checkll) {
    if (pos == 0) {
        return checkll && !(check4 == 1 && check8 == 1);
    }
    if (limit == 0 && lead == 0 && dp[pos][pre1][pre2][check8][check4][checkll] != -1) {
        return dp[pos][pre1][pre2][check8][check4][checkll];
    }
    long long up = 9;
    if (limit == 1) {
        up = num[pos];
    }
    long long ans = 0;
    for (long long i = 0; i <= up; i++) {
        if (lead == 1 && i == 0)  {
            ans = ans + dfs(pos - 1, pre2, i, limit && i == up, lead && i == 0, check8, check4, 0);
        }
        else if (lead == 1) {
            ans = ans + dfs(pos - 1, pre2, i, limit && i == up, lead && i == 0, check8 || i == 8, check4 || i == 4, 0);
        }
        else {
            ans = ans + dfs(pos - 1, pre2, i, limit && i == up, lead && i == 0, check8 || i == 8, check4 || i == 4, checkll || (i == pre2 && pre2 == pre1));
        }
    }
    if (limit == 0 && lead == 0) {
        dp[pos][pre1][pre2][check8][check4][checkll] = ans;
    }
    return ans;
}

long long solve(long long x)
{
    long long pos = 0;
    while (x != 0) {
        pos++;
        num[pos] = x % 10;
        x = x / 10;
    }
    return dfs(pos, 0, 0, 1, 1, 0, 0, 0);
}

int main() {
    long long x, y;
    cin >> x >> y;
    memset(dp, -1, sizeof(dp));
    cout << solve(y) - solve(x - 1);
    return 0;
}

参考文献

[0] 洛谷日报第84期
[1] 数位dp总结之从入门到模板

前言

题目1

题目描述

代码

分析

最高位标记limit

前导0标记lead

题目2

题目描述

代码

分析

题目3

题目描述

分析&&代码

题目4

题目描述

分析&&代码

参考文献

最高位标记`limit`

前导0标记`lead`