字符串匹配问题
字符串匹配,是指“字符串 P 是否为字符串 S 的子串?如果是,它出现在 S 的哪些位置?”的问题,其中S称为主串,P称为模式串。我们假设 S 串长度为 n , P 串长度为 m ,其中 n > m。
Brute-Force
容易想到朴素暴力匹配,从前往后逐字符比较,遇到不同的字符就continue ; P 串结束了返回 True , S 串结束而 P 串未结束返回 False 。具体流程如下:
- 枚举 $i\in[0,n-m)$
- 将 S[i] ~ S[i+m] 与 P 作比较。如果一致,则找到了一个匹配。
此方法被称为 Brute-Force 法,最坏的时间复杂度$O(nm)$。
例如:
主串:
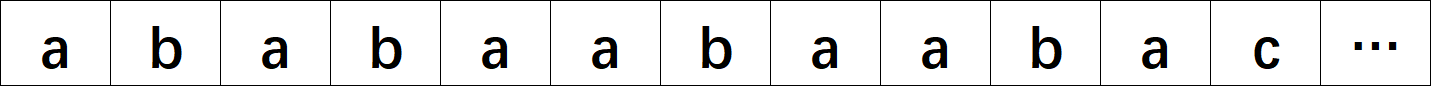
模式串:
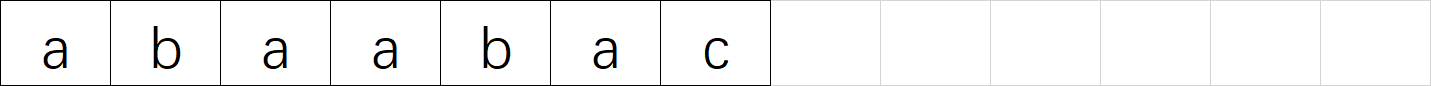
全匹配流程如下图所示:
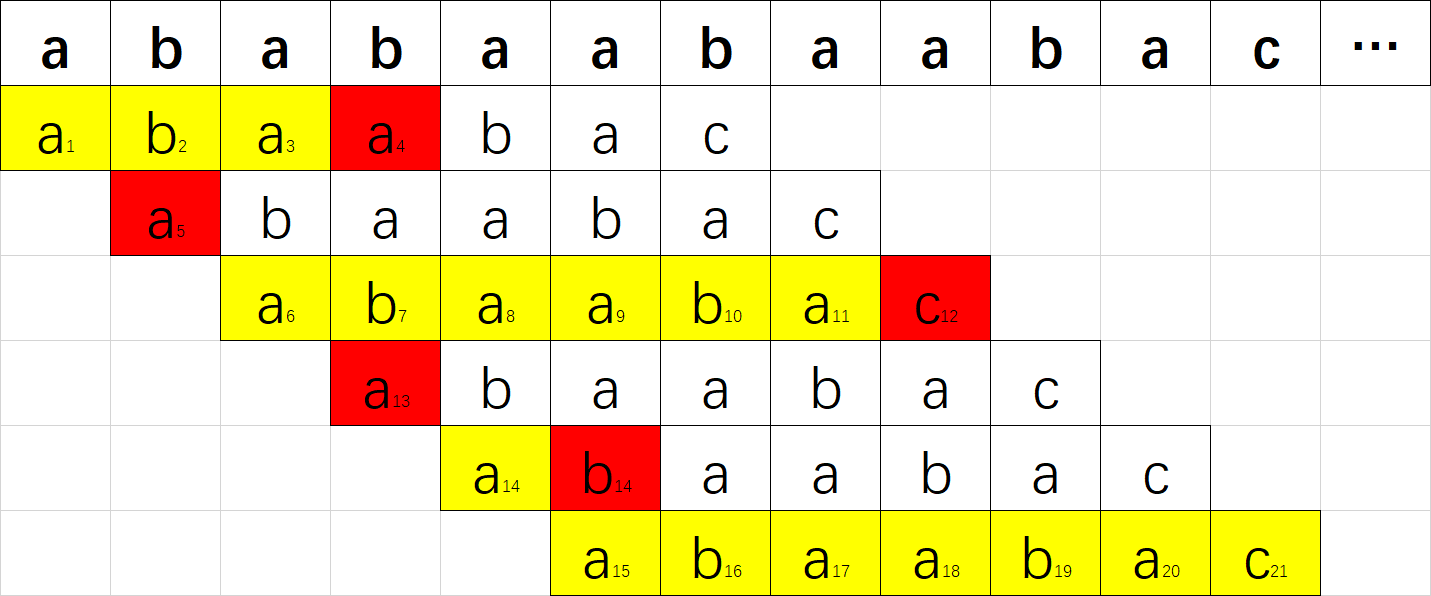
其中数字表示匹配的顺序。
改进的思路
我们无法改变 P 串或者 S 串的复杂度,因此只能在匹配次数上进行优化。可以发现,在 Brute-Force 算法中,在最坏情况下,例如S=”aaaaaaaaaab”,P=”aaaab”时,会进行 $n-m+1$ 次位移,每次位移最多会进行 m 次匹配,因此总时间复杂度是$O((n-m+1)*(m))$,也就是$O(mn)$的。
回到最初,我们需要实现的任务是“字符串匹配”,而每一次失败都会给我们带来一些信息——主串的某一个子串等于模式串的某一个前缀。这个前缀便是优化的关键之处。
next数组的引入
next数组是对于模式串而言的。 P 的 next 数组定义为: next[i] 表示 P[0] ~ P[i] 这一个子串,使得 前 k 个字符 恰等于 后 k 个字符 的最大的 k 。特别地, k 不能取 i+1 (因为这个子串一共才 i+1 个字符,自己肯定与自己相等,就没有意义了)。

上面给出了一个例子。P=”abaabac”时, next[4] = 2 ,这是因为 P[0] ~ P[4] 这个子串是”abaab”,前两个字符与后两个字符相等,因此 next[4] 取 2 。而 next[6] = 0 ,是因为”abaabac”找不到前缀与后缀相同,因此只能取0。
如果把模式串视为一把标尺,在主串上移动,那么 Brute-Force 就是每次失配之后只右移一位;改进算法则是每次失配之后,移很多位,跳过那些不可能匹配成功的位置。但是该如何确定要移多少位呢?
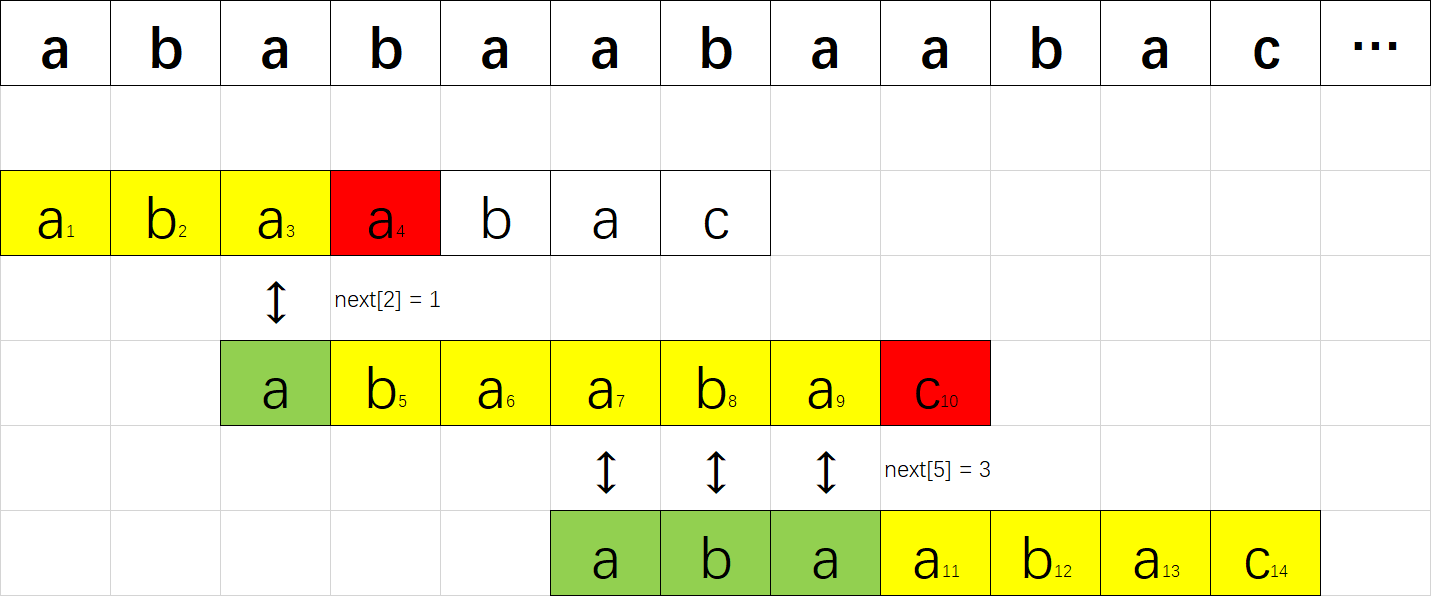
如上,在 S[0] 尝试匹配,失配于 S[3] <=> P[3] 之后,我们直接把模式串往右移了两位,让 S[3] 对准 P[1]。 接着继续匹配,失配于 S[8] <=> P[6], 接下来我们把 P 往右平移了三位,把 S[8] 对准 P[3]. 此后继续匹配直到成功。
我们应该如何移动这把标尺?很明显,如图中箭头所示,旧的后缀要与新的前缀一致(如果不一致,那就肯定没法匹配上了)!
回忆next数组的性质:P[0] 到 P[i] 这一段子串中,前 next[i] 个字符与后 next[i] 个字符一模一样。既然如此,如果失配在 P[r] , 那么 P[0] ~ P[r-1] 这一段里面,前 next[r-1] 个字符恰好和后 next[r-1] 个字符相等——也就是说,我们可以拿长度为 next[r-1] 的那一段前缀,来顶替当前后缀的位置,让匹配继续下去!
那么,如何分析这个字符串匹配的复杂度呢?乍一看,pos值可能不停地变成next[pos-1],代价会很高;但我们使用摊还分析,显然pos值一共顶多自增len(S)次,因此pos值减少的次数不会高于len(S)次。由此,不难分析出整个匹配算法的时间复杂度:$O(m+n)$。
求next数组
终于来到了我们最后一个问题——如何构建next数组。
回顾next数组的完整定义:
- 定义 “k-前缀” 为一个字符串的前 k 个字符; “k-后缀” 为一个字符串的后 k 个字符。k 必须小于字符串长度。
- next[x] 定义为: P[0] ~ P[x] 这一段字符串,使得k-前缀恰等于k-后缀的最大的k。
这个定义中,不知不觉地就包含了一个匹配——前缀和后缀相等。接下来,我们考虑采用递推的方式求出next数组。如果next[0], next[1], … next[x-1]均已知,那么如何求出 next[x] 呢?
来分情况讨论。首先,已经知道了 next[x-1](以下记为now),如果 P[x] 与 P[now] 一样,那最长相等前后缀的长度就可以扩展一位,很明显 next[x] = now + 1. 图示如下。
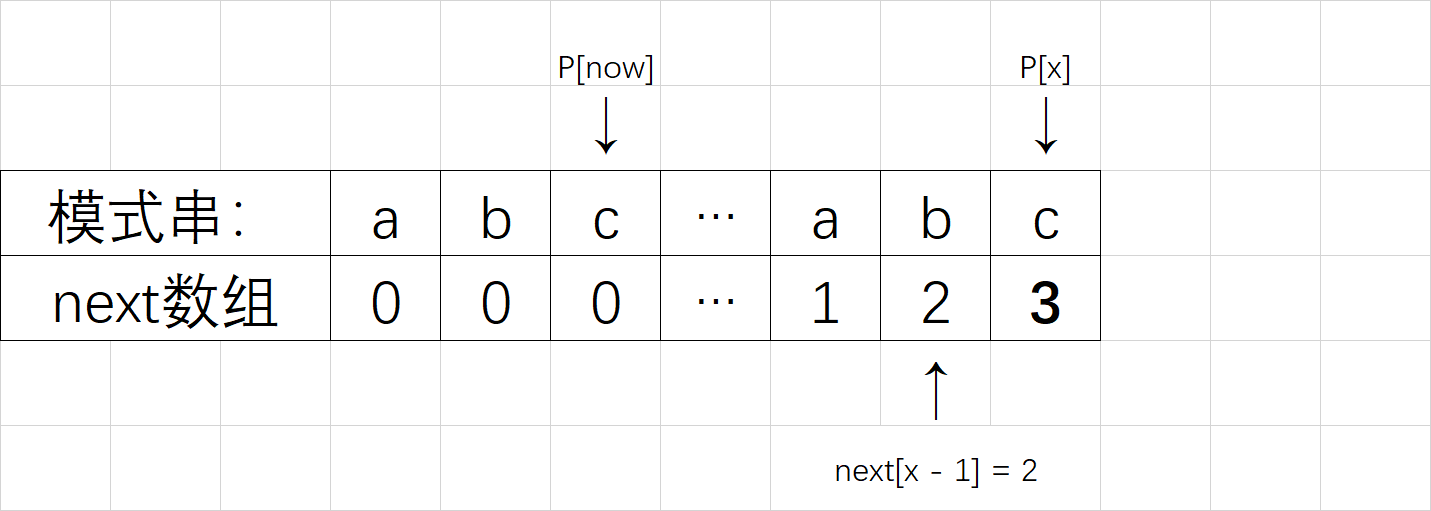
刚刚解决了 P[x] = P[now] 的情况。那如果 P[x] 与 P[now] 不一样,又该怎么办?
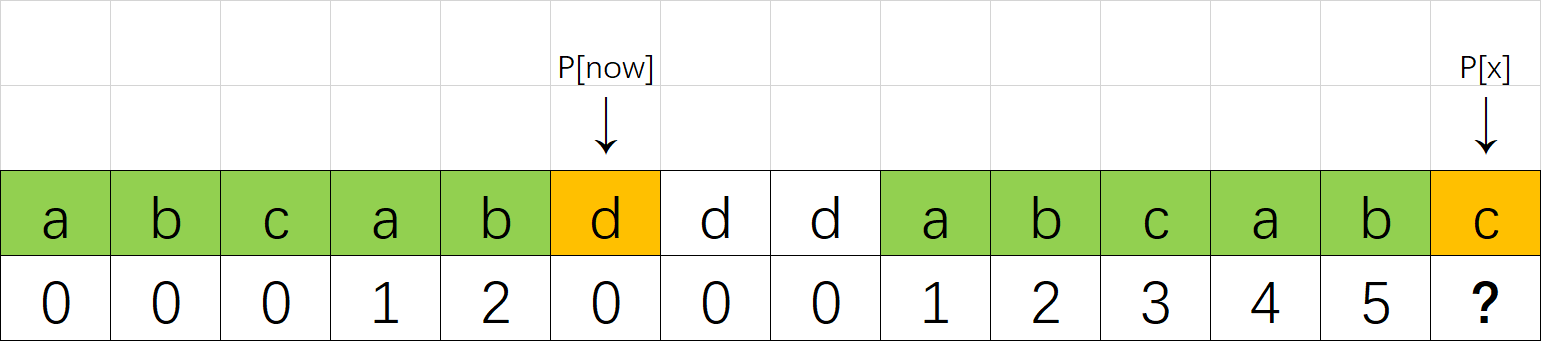
如图。长度为 now 的子串 A 和子串 B 是 P[0]~P[x-1] 中最长的公共前后缀。可惜 A 右边的字符和 B 右边的那个字符不相等,next[x]不能改成 now+1 了。因此,我们应该缩短这个now,把它改成小一点的值,再来试试 P[x] 是否等于 P[now].
now该缩小到多少呢?显然,我们不想让now缩小太多。因此我们决定,在保持“P[0]~P[x-1]的now-前缀仍然等于now-后缀”的前提下,让这个新的now尽可能大一点。 P[0]~P[x-1] 的公共前后缀,前缀一定落在串A里面、后缀一定落在串B里面。换句话讲:接下来now应该改成:使得A的k-前缀等于B的k-后缀的最大的k.
您应该已经注意到了一个非常强的性质——串A和串B是相同的!B的后缀等于A的后缀!因此,使得A的k-前缀等于B的k-后缀的最大的k,其实就是串A的最长公共前后缀的长度 —— next[now-1]!
把now更改为next[now-1]之后:
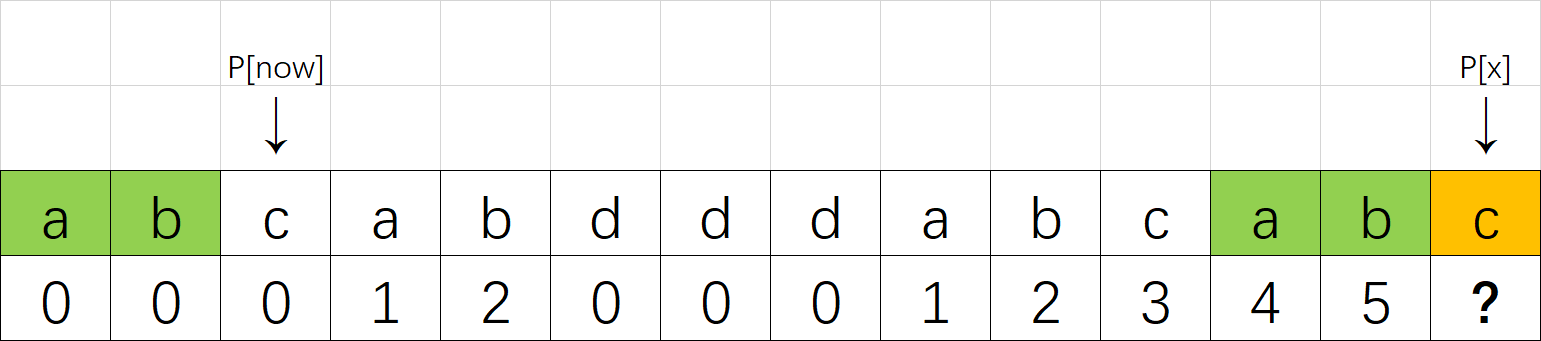
来看上面的例子。当P[now]与P[x]不相等的时候,我们需要缩小now——把now变成next[now-1],直到P[now]=P[x]为止。P[now]=P[x]时,就可以直接向右扩展了。
应用摊还分析,不难证明构建next数组的时间复杂度是$O(m)$的。至此,我们以$O(n+m)$的时间复杂度,实现了构建next数组、利用next数组进行字符串匹配。
最后是代码
(未审核,谨慎复制粘贴)
1 |
|